CS 180 Project 3: Face Morphing

Overview

This project explores face morphing techniques, including creating smooth transitions between faces, computing average faces, and generating caricatures. We'll go through several steps to achieve these fascinating visual effects.

Part 1: Defining Correspondences

In this initial step, we manually defined corresponding points on two images: Arnav's face (Image A) and Arush's face (Image B). These points mark key facial features like eyes, nose, mouth, and chin. We used the custom provided tool to select these points, ensuring consistent labeling across both images.

After defining the points, we computed a Delaunay triangulation to create a mesh over the faces. This triangulation is crucial for the warping process in later steps. scipy.spatial.Delaunay was used to triangulate each image, producing tri.

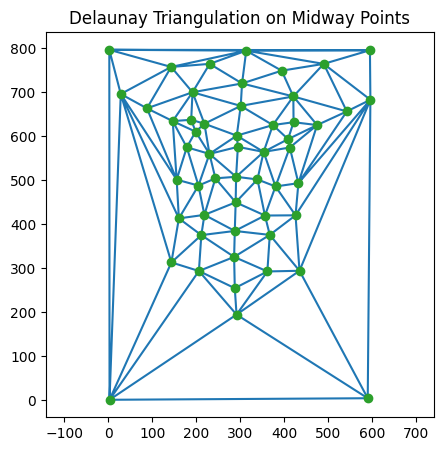
Part 2: Computing the "Mid-way Face"

The mid-way face represents the halfway point between two faces. To compute this:

To compute the midway face, we follow these key steps:

1. We start with two images and their corresponding facial landmark points.
2. We calculate the average shape by taking the mean of corresponding points from both faces.
3. For each triangle in the Delaunay triangulation of the face:
• We compute an affine transformation that maps the triangle from the source image to the average shape.
• We store this transformation for later use.
4. We then perform an inverse warp:
• For each pixel in the output image, we determine which triangle it belongs to.
• We apply the inverse of the stored affine transformation to find the corresponding pixel in the source image.
• We use either nearest neighbor or bilinear interpolation to sample the color from the source image.
5. This process effectively warps the source image to match the geometry of the average face shape.
6. By repeating this process for both input images and then averaging the results, we obtain the midway face.

This method ensures a smooth transition between facial features while maintaining a realistic appearance. The use of affine transformations for each triangle allows for local deformations that can accurately map one face shape to another.

The key to this process was implementing an affine warp for each triangle in our mesh.

Part 3: The Morph Sequence

We extended the mid-way face concept to create a full morph sequence. This involved implementing a morph function that produces intermediate frames between two images, controlling both shape warping and color blending independently.

The result is a smooth transition from one face to another, demonstrated in the following video:

Part 4: The "Mean Face" of a Population

We extended our morphing techniques to compute the average face of a population. Using the Danes Dataset, we:

1. Computed the average face shape of the population.
2. Morphed each face in the dataset to this average shape.
3. We repeated this process for the entire dataset, just for the males in the dataset and for just the females in the dataset.

Now we warp all the images in our dataset to the average shape of the entire population. Shown below are some of the examples of what happens to the faces in the dataset.

We now warp both images into each others' geometry to visualize what happens when we morph just the shapes.

Part 5: Caricatures

After computing the shape of the average face, we create caricatures by extrapolating from the mean. This process exaggerates the differences between an individual face and the average face, resulting in a caricature. The extrapolation is accomplished using the following formula:

Where:

• \(\text{img1}\) represents the individual face
• \(\text{avg}\) is the average face
• \(\alpha\) (alpha) is the exaggeration factor

This formula amplifies the differences in shape between the individual face and the average face. By adjusting the value of \(\alpha\), we can control the degree of exaggeration in the caricature. A larger \(\alpha\) value results in a more pronounced caricature effect.

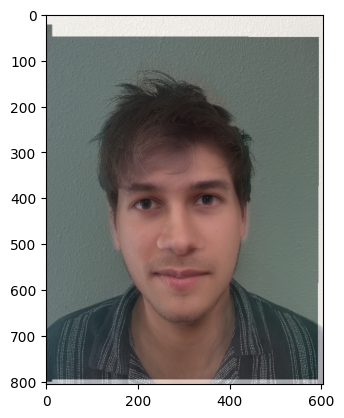
Part 6: Bells and Whistles: Changing Arnav's Gender using Average South Indian Female Face

In this part, we created a morph of Arnav and the average South Indian Female Face. We then manipulated the geometry of both faces onto each other, and then created a caricature of the female's face. We also generated a gif showing the morphing process.

We now warp both images into each others' geometry to visualize what happens when we morph just the shapes.

We also generated some caricatures using the same techniques as previously, as shown below.